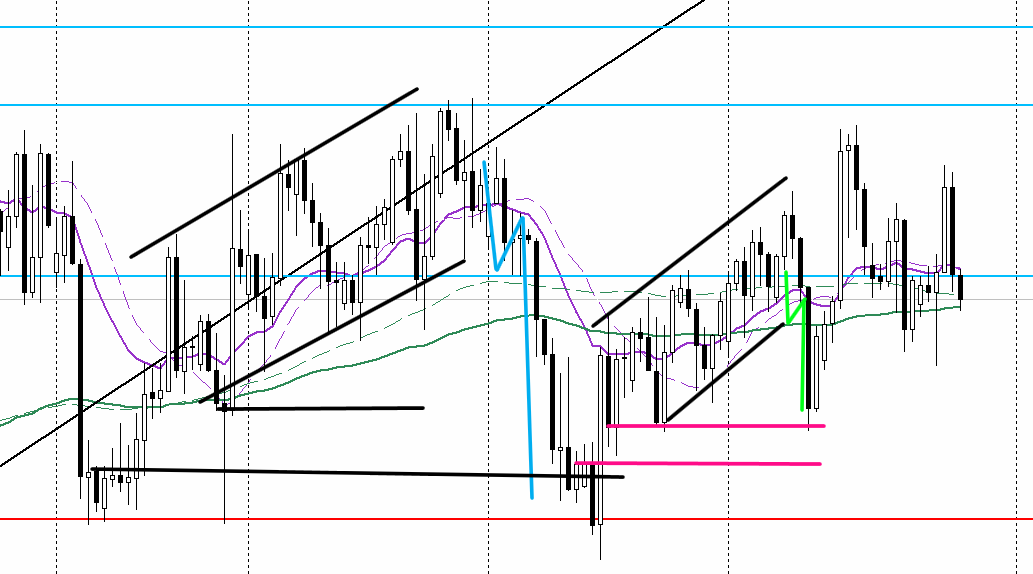
ポンドルの4Hチャート。黒チャネルからの緑色の下落は、青色の下落を再現している。

一般にフラクタル構造というと上位足での波形が下位足に再現されるというイメージだが、それは私の定義に当てはまらない。

チャートにおけるフラクタル構造とは過去時間に形成された波形がその時点より未来時間に再現されることだ。

その再現性においてサイズ感の矮小化と拡大化はまだ感覚的な部分であるが、１つはその元になった波形に対して再現される波形がどのようにして形成されているかで考えることができる。

今回の波は最初の波の安値から高値までの間において再現されている。つまり再現された波は最初の波、すなわち支配波の配下にあったということがいえる。その高値安値の範囲において再現されるものは基本的にその支配波のサイズ感を超えないので、狙うべき範囲も小さくなる。決裁位置は控えめに見ておくことが重要となる。

今回のこのチャートにおけるフラクタル構造はミラー効果といっても差支えないと思われる。特に今回のようなごく近い範囲における支配波内部での波形構造は、ミラー効果の定義に当てはめて考えることができると思う。

ミラー効果は同調効果ともいう心理学上の定義で、親密な関係では相手と同じ動作をすることが多くなるという動きに関わる概念である。

親密な関係というものをチャートに置き換えると、支配波の配下にあってその支配波とどれだけ近しい位置にいるかによって、その再現性の強度は変わると考えることができる。

今回の波形は、過去の値動きが未来の値動きを示唆する時、その波形が類似している事象をチャートにおけるフラクタル構造と認識する。という私の定義するフラクタル構造の概念と、今回発生したミラー効果による相乗効果によってその再現性が顕著になった例だと考える。

私はこうした波形認識を極めたいと思っている。そこのチャート形成の面白さが散りばめられていると思っている。だからやめることができないんだろう。